Reviewer(s) Corner
Read Recommendation from Alexander & Mike: highly recommended for self-supervised learning fans and everyone interested in representation learning
Writing Clarity: average plus
Prerequisite (prior knowledge):
- Probability and measure theory (basics)
- Main principles of supervised learning
Possible Practical Applications: Can be used to obtain powerful data representations from unlabeled datasets
Paper Details
- Download Link: https://arxiv.org/abs/2005.10242
- Code Link: https://github.com/SsnL/align_uniform
- Project Page: Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere (ssnl.github.io)
- Date & place of publication (last version): Arxiv, 07.11.2020
Paper Research Areas:
- Self-supervised learning
- Contrastive learning
Mathematical concepts, tools, and notations in the paper:
- Contrastive Loss
- Radial Basis Function Kernel
- InfoMax principle
- Weak convergence of probability measures
Introduction
Representation learning is an umbrella term for a variety of methods that allow us to build data representations that downstream tasks can benefit from. A great example of representation learning is word2vec - a self-supervised algorithm introduced in 2013 by Tomáš Mikolov and colleagues that uses a type of contrastive loss. The algorithm constructs word embeddings with certain desirable properties, e.g. words that have similar meanings are mapped to points that are close to each other in the embedding space. This property is also known as alignment. Transformer models extend word2vec capabilities and allow for context-dependent embeddings. This is great, but at the same time Transformer-generated embeddings suffer from a condition known as low uniformity - the embedding vectors tend to concentrate in a narrow cone of the embedding space (Mimno & Thompson, 2017; Ethayarajh, 2019) which leads to unwanted consequences (e.g. spurious similarities between unrelated words). Can we do better?
A summary of the paper
The authors demonstrate that contrastive loss implicitly optimizes two properties of data representations: alignment and uniformity. In addition, they introduce methods to measure these properties explicitly. Next, they propose a loss function that optimizes these properties and finally they show that this loss function can lead to results competitive with or better than the ones obtained using traditional contrastive losses.
The main ideas of the paper
Contrastive learning is one of the most widely used methods of constructing data representations (usually in a low-dimensional space, sometimes called latent space) of unlabeled data. The assumption behind this technique is that similar pieces of data have close representations, while dissimilar samples have distant representations. In particular, in most contrastive learning methods similar (positive) pairs of examples and dissimilar (negative), sample pairs are constructed during training. The contrastive learning objective usually aims to maximize the ratio of the distances between positive and negative pairs features. As an example, in computer vision applications, two different crops of the same image form a positive pair while randomly selected images make a negative pair.
In this paper, the authors examine the properties of self-supervised data representations trained via a contrastive learning procedure. The paper demonstrates that data representations (features) derived through the contrastive learning objective have two following properties:
- Alignment (closeness) between features of positive pairs of examples
- Uniformity (uniform distribution) of the data representation on the unit hypersphere (see the remark below). Intuitively, uniformity of feature distribution indicates that the data representations retain maximal information from the original data.
Remark: The paper imposes the unit-norm constraint on learned data features known for its ability to increase the training stability of contrastive learning methods (due to extensive usage of dot products). However, there is no rigorous proof of why the unit hypersphere constitutes a useful feature space property.
The main result of the paper states that the contrastive learning objective directly optimizes both aforementioned properties when the number of negative samples reaches infinity. Simply put, when the number of negative examples in a batch is high, optimizing the contrastive loss objective leads to aligned and uniformly distributed data representations.
It is known that increasing the number of negative examples in contrastive learning methods usually results in better data representations. From this perspective, replacing a contrastive learning objective with a combined uniformity and alignment objective may be able to extract more powerful data features. To impose uniformity and alignment properties on data representations, the authors introduced theoretically-anchored metrics to measure their (representations’) alignment and uniformity. Finally, the paper showed that incorporating these metrics into the representation learning objective together with the contrastive loss, produced better data features.
The image below illustrates the strong alignment and uniformity properties of data representations learned through unsupervised contrastive learning (2 leftmost images at the bottom). Interestingly, features learned in a supervised learning regime also exhibit a high degree of uniformity and alignment (2 leftmost images in the middle).

A piece of intuition
Let’s try to provide some insight into why alignment and uniformity can be natural properties of data representation, derived through the contrastive loss objective. We start with the following (the most widely used) form of contrastive loss:

Assuming positive examples have the same representation/are perfectly aligned (with a dot product equal to 1, since they both have a unit norm) the above expression becomes:

When the number of negative examples M is very large, the minimum of the last expression is attained when pairwise distances between data representations are maximal (dot product at the exponent is as close to zero as possible). So alignment and uniformity appear to be natural properties of good data representation (attains small value of the contrastive loss).
Main Theorem
Now let's discuss the main theorem of the paper:
The theorem states that the contrastive loss is equal to the sum of 2 terms for several negative examples M approaching infinity (a bit simplified for clarity)
Term1: Is minimized for the perfectly aligned data (representations of all positive pairs are the same).
Term2: Is minimized when data representation is uniformly distributed.
Training aligned and perfectly distributed features:
So it appears that replacing the contrastive loss with uniformity and alignment objectives leads to more powerful data representations. The question is how do we train the model to extract features that possess these properties? The authors propose to enforce feature alignment and uniformity by using the following losses:
Alignment: alignment loss is defined by an average distance between features of positive samples pairs
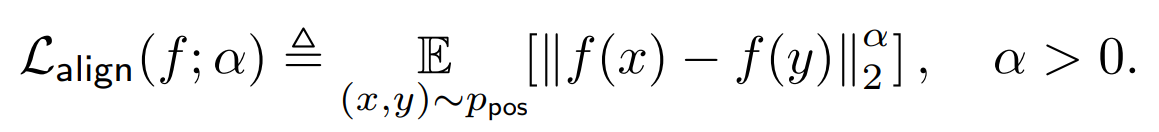
Uniformity: To impose uniformity on data features, the authors use the so-called Gaussian Radial Function (also known as radial basis function or RBF) kernel. With RBF, the distance between feature vectors x and y is defined as:
Note that the second equality follows from the unit norm of x and y. Now uniform loss, function, based on RBF has the following form:
But how is this RBF-based loss connected to feature uniformity? It turns out (the paper proves it) that uniform feature distribution on the unit hypersphere minimizes the RBF-based loss function. Simply put, for very large sample size, feature vectors minimizing the uniformity loss function will “cover the unit hypersphere surface nearly uniformly”.
Remark: Both the uniformity and alignment losses are less computationally expensive than the vanilla contrastive loss due to the absence of softmax operation,
Therefore training a neural network with a combination of the above-explained loss functions seems like a reasonable way to obtain uniformly distributed and aligned features.
Paper Achievements
The authors found that the proposed uniformity/alignment loss (and combined the vanilla with contrastive loss) is capable of extracting more powerful features, resulting in better performance on downstream tasks (classification and depth estimations) on several datasets (including NYU Depth V2, ImageNet, ImageNet100, BookCorpus)
Post Scriptum
For a long time, alignment and uniformity have been recognized as good properties of data representations. This paper found several connections between well-known unsupervised contrastive learning techniques and these data feature properties.
#deepnightlearners




